Davide Legacci | Research Blog

Tags: game-theory, learning-in-games

An example of a game which is at the same time zero-sum and potential.

A potential zero-sum game

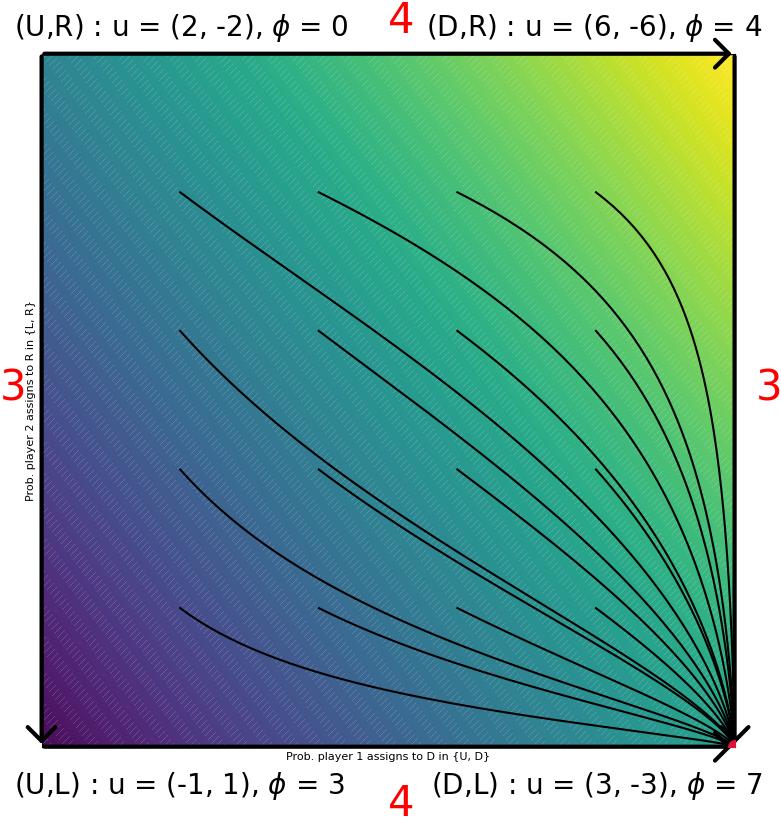
Consider the zero-sum $2\times 2$ game with payoff bimatrix given by

\[u_1 = \begin{pmatrix} -1,1 & 2,-2 \\ 3,-3 & 6,-6. \end{pmatrix}\]

It’s easy to check that the game is potential with potential function

\[\phi = \begin{pmatrix} 3 & 0 \\ 7 & 4 \end{pmatrix},\]

and that $(\text{down}, \text{left})$ with outcome $(3, -3)$ is strict Nash. Since the game has non-trivial unilateral deviations it is not strategically equivalent to the zero-game, thus showing that the spaces of zero-sum and potential games intersect non-trivially, even after quotienting away strategical equivalence.

The image below shows the response graph of the game and some trajectories of replicator dynamics converging to the strict Nash equilibrium.