Davide Legacci | Research Blog

Tags: geometry

An exercise on submanifolds arising as regular level sets of smooth maps¹.

An exercise on regular level sets

$\newcommand{R}{\mathbb{R}}$

Let $F: \R^3 \to \R^2$ be $F(x, y, z) = (x^2, y^2-z^2)$. Its differential $dF_{(x,y,z)}: R^3 \to \R^2$ is the linear map

\[dF_{(x,y, z)} = \begin{pmatrix} 2x & 0 & 0 \\ 0 & 2y & -2z \end{pmatrix}.\]

A point $p \in \R^3$ is a critical point for $F$ if $dF_{p}$ is not surjective, i.e. if $\text{rk}({dF_p})<2$.

A point $(\alpha, \beta) \in \R^2$ is a critical value for $F$ if its level set $F^{-1}(\alpha, \beta)$ contains a critical point. By the regular level set theorem, if $(\alpha, \beta)$ is not a critical value – i.e., its level set $F^{-1}(\alpha, \beta)$ does not contain critical points – then $F^{-1}(\alpha, \beta)$ is a submanifold of $\R^3$ of codimension $2$.

The critical points for $F$ are $(0, y, z)$ for all $y, z \in \R$; and $(x, 0, 0)$ for all $x \in \R$. Thus for all $\alpha >0$ and $\beta > 0$, the value $(\alpha, \beta) \in \R^2$ is regular and its level set $S = {(x, y, z): F(x, y, z) = (\alpha, \beta)}$ is a non-empty $1$-dimensional submanifold of $\R^3$ given in parametric form by

\[\begin{split} x^2 &= \alpha, \\ y^2-z^2 &= \beta. \end{split}\]

This is a disconnected manifold given by $4$ hyperbole branches:

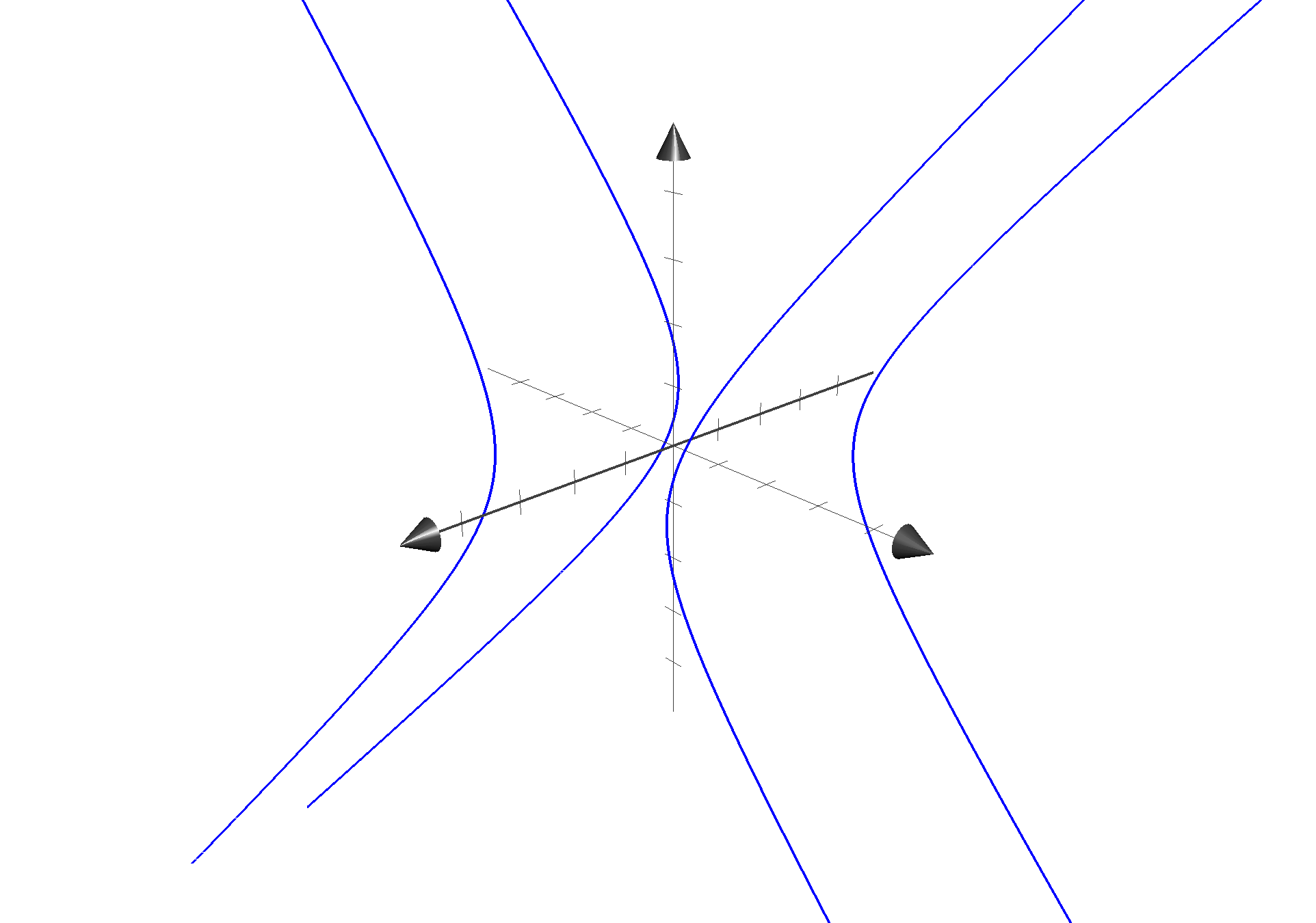
The branch with $x > 0$ and $y > 0$ is parametrized by $\psi: \R \to \R^3$ with

\[\psi(t) = (x,y, z)(t) = (\sqrt{\alpha}, \sqrt{\beta + t^2}, t).\]

Differentiating the parametrization with respect to $t$ gives the vector field $\partial_t$ spanning the tangent space to $S$ at $t$ as a linear combination of the basis vector fields $\partial_x, \partial_y, \partial_z$: we get $\partial_t = (0, z/y, 1)$, so the affine tangent space to $S$ at $(x, y, z)$ is

\[\tilde{T}_{(x,y,z)}S = T_{(x,y,z)}S + (x,y,z) = \langle(0, z, y)\rangle + (x, y, z).\]

For example for $t = 1$, $\alpha = \beta = 1$, $(x, y, z) = (1, \sqrt{2}, 1)$, we get

\[\tilde{T}_{(1,\sqrt{2},1)}S = \langle(0, 1, \sqrt{2})\rangle + (1, \sqrt{2}, 1).\]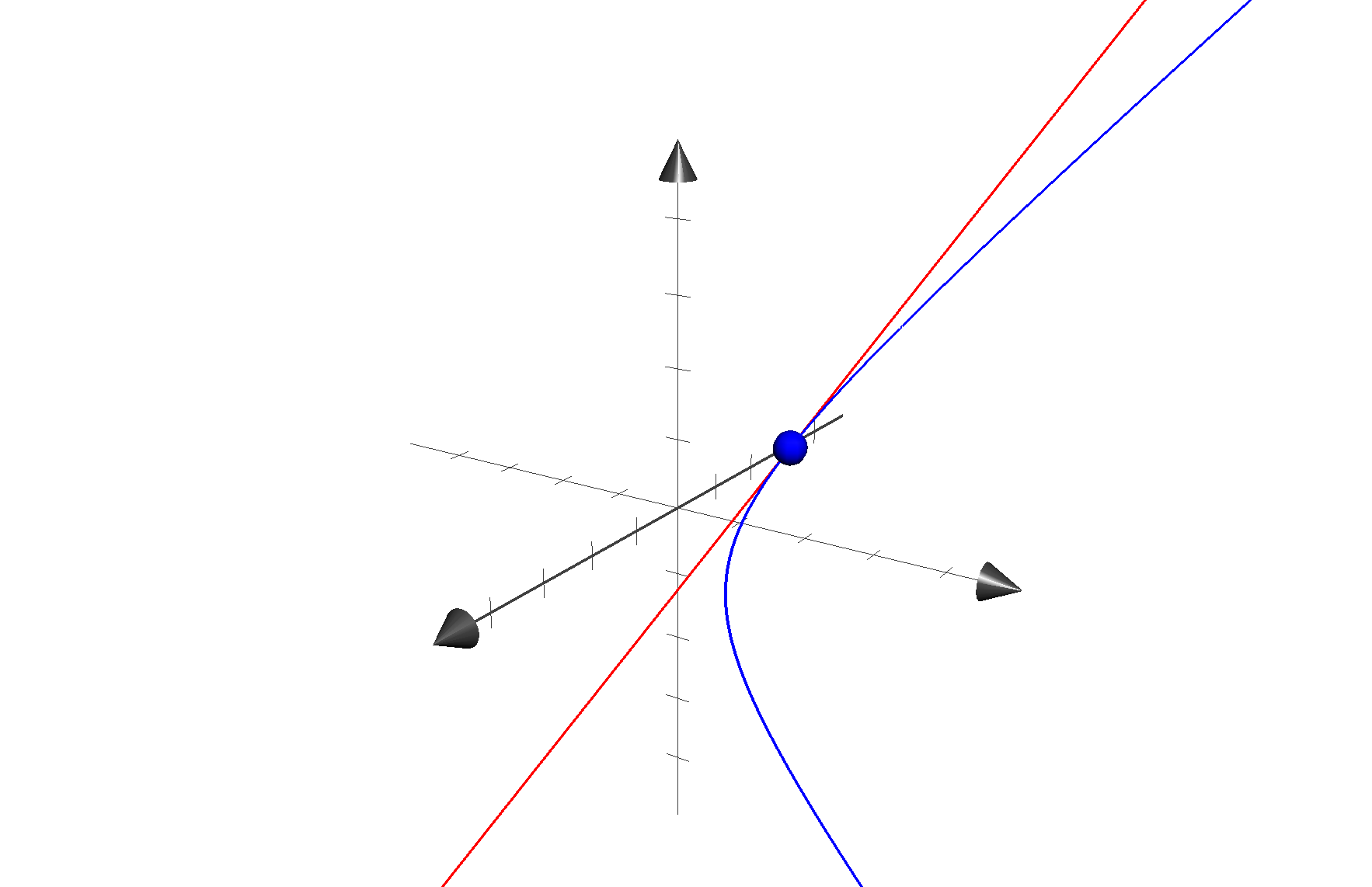

1. J. M. Lee, Introduction to Smooth Manifolds, 2nd ed. in Graduate Texts in Mathematics. Springer-Verlag New York, 2012. ↩